【FXボリンジャーバンド】が採用している標準偏差の意味を徹底解説!
ボリンジャーバンドというインディケーターには標準偏差という概念が入っている。では一体なぜボリンジャーバンドは標準偏差という考え方を取り入れているのか。そこを徹底解説する。
Table of Contents
標準偏差とは?

左側の表はあるクラスのテストの平均であり、この平均から正確なばらつきを求めていく。
このばらつきを見るのが標準偏差であるが、段階的に見ていく。
データのばらつきを求めるには兎にも角にも平均を求めることから始めるが、この場合の平均点はA君~G君の点数を合計してデータ数7で割る。すると平均点80点が算出された。
次に各データが平均点からどれだけ離れているかをみればそのばらつきが取れる。
ちなみにデータの、平均点からどれだけ離れているかの乖離のことを偏差という。
この場合の偏差はどうなるかというと、上図の「偏差」の欄の通りになる。
ここで偏差が出たので、この偏差の平均を求めれば、偏差のばらつきを求めることができるようになるのだが、この偏差の欄を合計すると0になってしまい、平均を求めることができなくなる。
この問題を解決するために用いるのが絶対値という考え方である。
標準偏差の大きな特徴
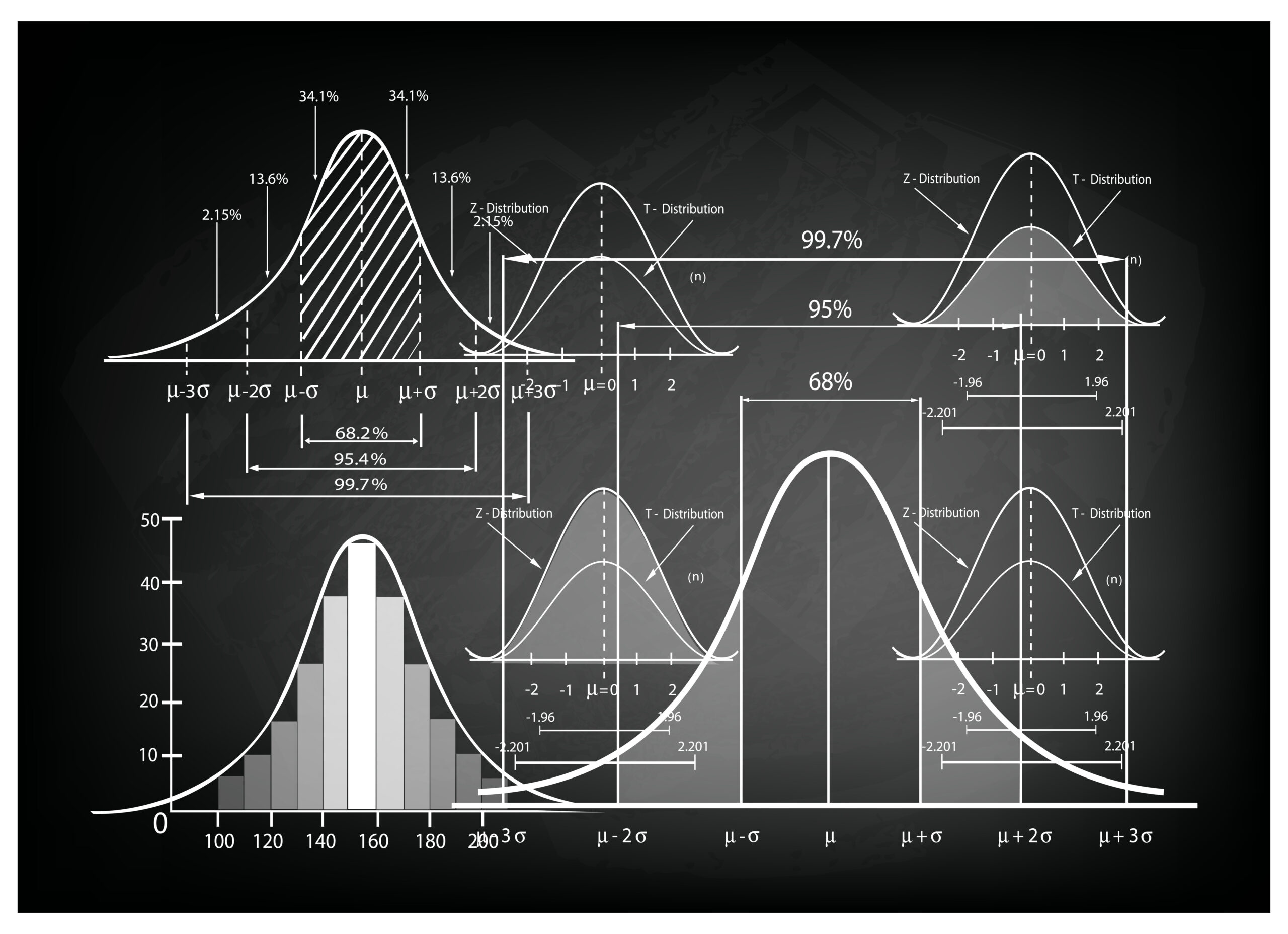
データが正規分布の場合には、±1σ~±3σの間にデータが収まる確率が68.3%~95.4%もしくは99.7%である。
これがボリンジャーバンドの唯一の統計的な要素である。
正規分布の場合のみ標準偏差の有用性が発揮されるが、先ほども述べたようにマーケット価格は正規分布には当てはまらない。
だとするならば、標準偏差の要素を用いたボリンジャーバンドは有効ではないのかというと決してそうではない。
ボリンジャーバンドならではの有効性があるのでその有効性を理解するためにはこの計算式から理解する必要がある。
左側の表はあるクラスのテストの平均であり、この平均から正確なばらつきを求めていく。
このばらつきを見るのが標準偏差であるが、段階的に見ていく。
データのばらつきを求めるには兎にも角にも平均を求めることから始めるが、この場合の平均点はA君~G君の点数を合計してデータ数7で割る。すると平均点80点が算出された。
次に各データが平均点からどれだけ離れているかをみればそのばらつきが取れる。
ちなみにデータの、平均点からどれだけ離れているかの乖離のことを偏差という。
この場合の偏差はどうなるかというと、上図の「偏差」の欄の通りになる。
ここで偏差が出たので、この偏差の平均を求めれば、偏差のばらつきを求めることができるようになるのだが、この偏差の欄を合計すると0になってしまい、平均を求めることができなくなる。
この問題を解決するために用いるのが絶対値という考え方である。
すると、先ほどの偏差を絶対値にしてあげたもの、つまりマイナスだったもののマイナスをとってあげたもの、これが表の3列目ということになる。
よって、偏差の絶対値の合計は、76となり、これをデータの数である7で割ると平均が10.86となる。
このような形で絶対値を用いて絶対値の合計をデータ数で割ったものを平均偏差という。この平均偏差もデータのばらつきを求める尺度の一つとなる。
↓↓↓ボリンジャーバンドの記事は以下をクリック ↓↓↓
平均偏差を使うとこのような値が求められるが、ここで1つ疑問が生じる。なぜ、ボリンジャーバンドは平均偏差ではなく標準偏差を使っているのか。
平均偏差の問題点

平均偏差はばらつきを捉える一つの尺度ではあるものの、これはこれで問題点があるからだ。上の図は偏差の合計が同じデータを2つ並べたものである。左側は偏差の合計150となる。それぞれ平均点50点から+25離れているもの、-25離れているものがあり、データの数は6個ある。
図の右側は、平均は同じ50点だが、それに対する偏差はそれぞれ異なる。一番小さな偏差だと15、一番大きなものだと30になる。しかし、右と左のデータは、ばらつきは違うものの偏差の合計は一緒で平均偏差も同じになる。これが平均偏差の問題点となる。
標準偏差の2乗・分散の考え方

平均偏差の問題点を解決する目的で2条というものを活用したものとなる。表示しているデータは先程と同じである。2乗とはある値を2回かけることで2の2乗は4、3の2乗は9となる。先程の左側のデータ+25、-25とデータが並んでいたが、25×25で全て625となる。それぞればらつきのあったデータもそれぞれ2乗したデータとなる。
2乗するメリット
これは、プラスもマイナスも2乗するので、どんな値もプラスになる。正の値で統一ができる。2乗する分データの数が大きくなるので、ばらつきを正しく評価できる。わかりやすく言えば、偏差が2と4のデータがあったとすると、平均偏差ではその差は2倍であるが、これを2乗することで2×2=4、4×4=16ということで4倍の違いが出てくる。2乗することでポイントを高く見積もることができる。
すると、先程平均偏差が同じとなったデータに若干の違いが出た。
・右側の偏差の合計4132 平均689
このように、2乗したデータの平均を取ることを分散という。これも先程の平均偏差と同様データのばらつきを見る尺度である。
分散の問題点
平均偏差を上回ったかに見える分散だが、これにも問題点がある。2乗する分だけデータが大きくなってしまうことである。これだけ小さい数値ならば計算するのに苦はないと思うが、データの対象が年収であったり、都内の不動産価格のばらつきを見ようと思ったときには値が大きいので2乗すると桁が変わってしまったり、する問題が生じるので不便である。そこでこの分散の問題点を解決するのに使用するのが平方根というものになる。
この平方根を用いるメリットは、2乗して大きくなり過ぎた値というのをその分散の特性を残しながら小さくできることだ。
標準偏差の求め方を最初から解説

上の表から標準偏差を最初から算出してみよう。これは、あるクラスのテストの点数である。このクラスのテストの点数のばらつきを見ようと思うと、まずは平均点を求めることから始める。
90~85までのデータをすべて合計し、データの数10で割ると71.2点という平均点が求められる。それからばらつきを求めようとすると、偏差ー各データが平均点からどれだけ離れているかーを求めていく。
B→74-71.2=2.8
C→87-71.2=15.8
D→71-71.2=-0.2
E→59-71.2=-12.2
F→65-71.2=-6.2
G→61-71.2=-10.2
H→69-71.2=-2.2
I→51-71.2=-20.2
J→85-71.2=13.8
以上のように各データに対する偏差が求められた。
ただ、この偏差の段階では、プラスの合計とマイナスの合計を足すと0になるという問題点が生じるため、2乗という概念を用いる。
B→(2.8)²=7.84
C→(15.8)²=110.6
D→(-0.2)²=0.04
E→(-12.2)²=148.84
F→(-6.2)²=38.44
G→(-10.2)²=104.04
H→(-2.2)²=4.84
II→(-20.2)²=408.04
J→(13.8)²=190.44
これらの正の値で統一した数の平均、つまり分散を求めると、150.56となる。しかし分散はこの程度のテストの点数なら問題ないが、2乗する分データが大きくなりすぎるという問題があることから、この値の平方根(ルート)をとることによってデータを小さくする。すると標準偏差12.27028932が求められる。
標準偏差まとめ
以上のことから、平均から平均偏差を求めてその後分散というプロセスを経て、それぞれの問題点を解決して最終的に算出される標準偏差がばらつきを求めるのに一番適したものであるということがはっきりするだろう。
したがって、ボリンジャーバンドにもその標準偏差が採用されている。ボリンジャーバンドからわかることはミドルバンドから見た方向性ばかりではなく、直近一定期間の価格のばらつきつまりボラティリティをより詳細に把握できるインディケーターと言える。




